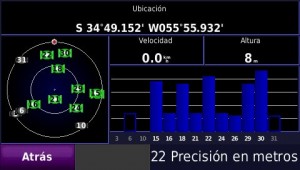
Sin rectángulo: (icono de satélite gris). Detecto al satélite, pero aun no cargo ni calendario ni efemérides.
Rectángulo vacío: Tiene cargado el calendario de ese satélite. (titila el icono con el numero del satélite hasta que termine de cargar efemérides).
Rectángulo lleno: Tiene cargado el calendario de ese satélite + efemérides. (fijo el icono y color). No toma posición hasta que por lo menos capte 4 satélites con efemérides incluidas. Porque 4? es más técnico, después lo explico.
La altura del rectángulo representa la intensidad de la señal que está recibiendo, pero no sirve de nada si no está completa con efemérides incluidas y tres satélites más en las mismas condiciones. La precisión de posicionamiento no tiene relación directa con la intensidad de la señal aunque importa, también depende de la distribución geométrica de los satélites en el cielo, rebotes y varias cosas más.
El GPS recibe las señales de los satélites. El GPS sabe a qué velocidad viajan las señales y en qué posición están los satélites (esto último porque el aparato se “baja” de los satélites las efemérides del mismo, es decir, donde va a estar en cada momento). Es decir, la distancia a los satélites se mide cronometrando las señales transmitidas por los satélites hasta el receptor. Dado que la velocidad de la luz es elevada, es necesario saber con mucha precisión el momento en que el satélite emitió la señal y el momento en que el GPS la recibió, para que la distancia y después la posición sean calculadas con precisión. Cada satélite lleva en su interior un par de relojes atómicos. Los GPS al contrario, tienen un relojito barato en su interior. Por esto, vamos a tener un error de timing cuando la señal llegue al receptor. Ahora, las señales que llegan de los satélites la medimos al mismo tiempo, y suponemos (correctamente) que todas tienen el mismo error por esto, y debemos calcular este error para poder determinar una posición precisa. En suma, para calcular esta posición tenemos que resolver cuatro incógnitas: el error del reloj del receptor y las tres coordenadas espaciales. Por lo tanto, tenemos que medir las distancias de al menos cuatro satélites para tener las cuatro ecuaciones para poder resolver las cuatro incógnitas. Por esto es que los satélites están dispuestos de tal manera que siempre haya a la vista al menos cuatro, en cualquier lugar de la Tierra.
Los satélites giran más rápido que la tierra aproximadamente al doble de la velocidad de esta, ellos dan una vuelta cada mas o menos 12 horas si estuvieran a 36000 Km estarían en órbita geoestacionaria y mas allá girarían más lento. Con respecto a la cantidad con tres es suficiente para el plano para el espacio te voy a hacer una comparación que leí por ahí. Si quiero saber mi posición sabiendo la distancia hasta un satélite cuya posición conozco, puedo imaginar una esfera y yo puedo estar en cualquiera de los infinitos puntos que la forman, si tengo una segunda mi posición se “restringe” (jaja siguen siendo infinitos) a los infinitos puntos del circulo producto de la intersección de ellas, si agrego un tercer satélite con su esfera imaginaria mi posición ahí si se restringe a dos puntos que son producto de la intersección de esta última con el circulo anterior, y acá podríamos parar porque un punto estará sobre la superficie terrestre pero el otro no, pero si quiero que me quede uno solo entonces necesito un cuarto satélite, el que le llamo mágico porque convierte el reloj interno de tu GPS en uno de precisión atómica.
Además de todo esto, aclaro algo mas para que se entienda lo de los círculos.
Imaginemos que estamos en el medio del océano, el horizonte es un círculo que nos rodea, el mismo está representado por el circulo mas grande. Si miramos el horizonte en un punto cualquiera, subimos la mirada 45° y ahí imaginamos otro círculo en el cielo paralelo al anterior, ese es el círculo más pequeño.
El punto rojo no es otra cosa más que el rumbo, es decir representa el punto hacia el cual vamos.
La ultima, los satélites que se encueran dentro del circulo pequeño, aportan menos exactitud en el posicionamiento, simplemente por un tema de geometría, los que están entre los dos círculos tienen más exactitud por el fenómeno inverso al anterior pero como las ondas emitidas por ellos entran con ángulos pequeños a la atmósfera terrestre (todas sus capas y también la estratosfera) estas se ven perturbadas y terminan por ser imprecisos. Este error se minimiza con la corrección diferencial (WAAS, EGNOS, SBAS) y puede llegar a ser submetrica.